Rietveld Fitting with Rigid Bodies
Introduction
It is a common
situation that a powder diffraction dataset will not provide enough
observations to allow refinement of all atoms independently. This is not only a
problem for powder diffraction; it is usually the case in single-crystal
protein structure determination as well, as few datasets for that can be
collected to atomic resolution. When the number of parameters is not sufficient
to discern individual atomic positions, it is necessary to apply constraints and/or
restraints. Constraints simplify the crystallographic model by reducing the
number of parameters. Restraints treat assumptions about the model as experimental
observations. Examples of restraints
include providing target values for bond distances and angles, or penalizing a
refinement if atoms diverge from a plane. One common constraint is to group Uiso values so that a single value is used for
all atoms of a particular type or in a common bonding environment.
One of the more
powerful types of constraints in GSAS-II is to constrain a group of atoms so
that their relative positions are fixed. Such a group of atoms is known as a
rigid body. The core concept behind rigid body refinement is that 3 parameters define
an origin and only 3 orientation parameters are needed to locate a rigid body,
so that only 6 parameters are needed to locate and orient the body, though in
some cases symmetry will constrain some of these values and the number of
refinable parameters will thus be reduced. In contrast, 3 position parameters
are needed for every atom in a structure on a general position. Thus, a
four-atom group requires 12 positional parameters and a 6-atom group requires
18 positional parameters, when modeled with individual atoms, but as
rigid-bodies only 6 parameters will be needed. Also, since the relative
positions are fixed, rigid bodies result in a more chemically reasonable structure.
GSAS-II offers two
types of rigid bodies. This tutorial will demonstrate use of one type, residue
rigid bodies, which allow incorporation of optional torsional parameters.
The second type, vector rigid bodies, offer one or more refinable size
parameters, which can allow for refinement of selected bond distances or
geometrical factors, but this is less commonly needed, compared to torsions.
In the supplied
example GSAS-II project file, a powder diffraction dataset is supplied for a
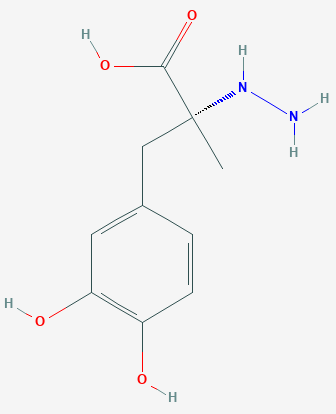
sample where there are two independent copies of the chiral R-(+)-Carbidopa
molecule (shown below) as well as two water molecules in the asymmetric
unit.
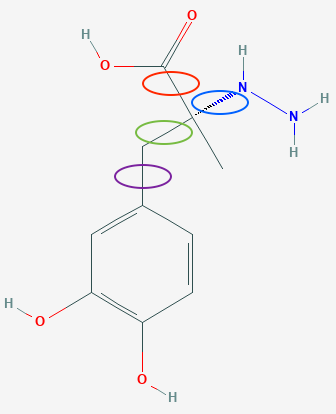
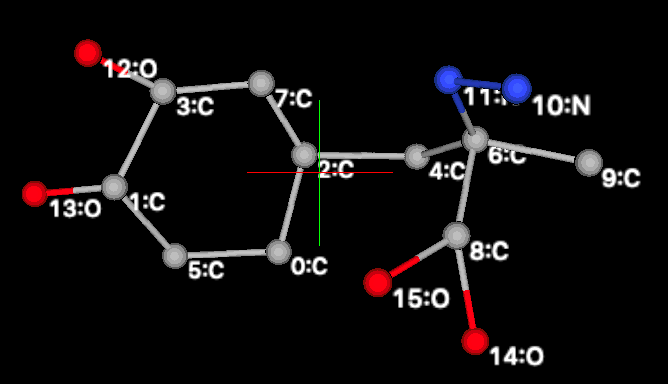
Since chemical
knowledge dictates that the 6 atoms in the phenyl ring, as well as the 6 atoms
bonded to them, will lie in a plane, and since bond distances and angles are
well known for those atoms, there is no reason to give these atoms any degrees
of freedom in the model used to fit the diffraction data, beyond the
orientation and position of the group. The positions for the remaining non-H
atom can be determined with only 4 additional parameters, noting that rotation
is possible around the four bonds circled below.
Thus, all 16
non-hydrogen atoms can be positioned with 10 parameters: 3 coordinates, 3
orientation parameters and 4 torsions. This is almost a five-fold
simplification compared to the 48 positional parameters needed for 16
unconstrained atoms. If we had neutron data that would allow location of
hydrogen atoms, adding 5 more torsions would allow for the hydrogen atoms to be
positioned as well, where a total of 30 atoms would be located from 15
parameters.
In this example, the
fit in the supplied GSAS-II project file appears quite good with respect to the
agreement to the observed data, but closer examination shows that the bond
distances and angles of the two molecular groups are quite irregular. Since
this distorted structure is not physically reasonable, this model is not
acceptable. This well-fitting but poor-quality model arises because too many
parameters were introduced, which is sometimes called overfitting. In this
tutorial, a better model will be developed using rigid bodies for the two
molecules, providing a more chemically reasonable representation with fewer
parameters -- simply a better fit.
Step 1. Export Cartesian coordinates for R-(+)-Carbidopa
from a crystal structure
There are two steps
to working with rigid bodies in GSAS-II. The first is to obtain an accurate set
of coordinates for the molecule, molecular fragment, or ionic moiety, which can
be done in a number of ways. One way is to locate an accurate crystal structure
from a database or paper. A second method is to use a computational tool to
determine an approximate structure regularized for reasonable bond lengths.
This can be done with low-accuracy forcefield computations or varying levels of
improved theory. A good tool for simple forcefield minimization is the free
cross-platform Avogadro program.
Note that we could
generate the R-(+)-Carbidopa fairly simply from inside Avogadro by drawing the
molecule (process described
here), or even quicker, since the PubChem entry lists
a
SMILES description of the atomic bonding
[C[C@@](CC1=CC(=C(C=C1)O)O)(C(=O)O)NN], that description could also be used
using the Avogadro Build/Insert/SMILES… menu command, but in this step we will
use a more general method to input a molecular fragment to Avogadro, so that it
can be regularized.
1A) For this tutorial, we will export coordinates
from GSAS-II in a form to be read Avogadro. They will be regularized in the
next step.
Begin by starting
GSAS-II. Any .gpx file (GSAS-II project) may be
used. If a new, empty, project is used, select the Data/“Add
new phase” menu item first. Select the Rigid Bodies tab in the data
tree.
1B) Use the “Edit Vector Body”/“Extract
from file” menu item select
the GSAS-II gpx format and read in the distort1.gpx file included in the sample input. This will read in the
coordinates for 34 atoms (two carbidopa molecules and two O atoms), from this
we want to select only one carbidopa molecule.
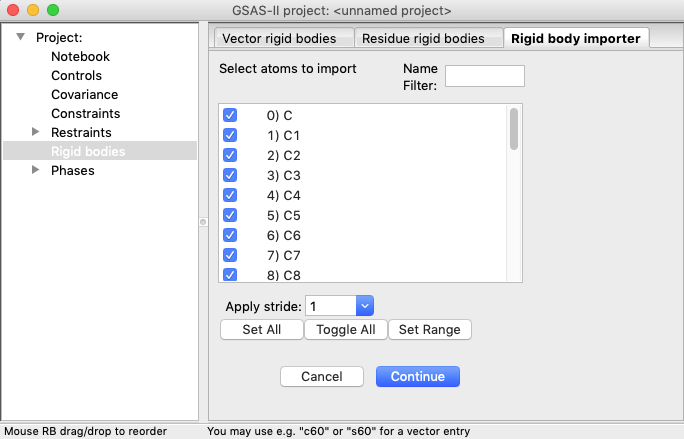
1C) Unselect all atoms by pressing the Toggle
All button and then select the first sixteen atoms using the “Set
Range” button and selecting the first [“0) C”] and the sixteenth atom [“15)
O3”]. Note that in the plot of the structure, unselected atoms appear partially
“greyed out” compared to selected atoms.
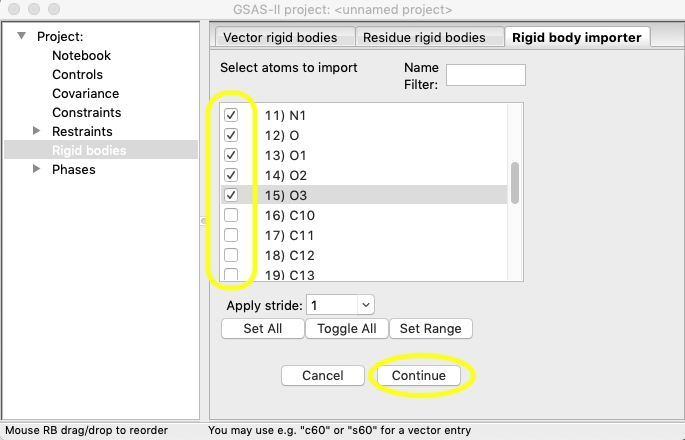
Once the 16 atoms
are selected, press “Continue”. The rigid body then appears in the plot
window. Note how distorted the molecule appears.
1D)
If these coordinates were
satisfactory, the rigid body could be created at this point, but since these
coordinates are distorted, we will regularize them in Avogadro first. Export
the coordinates by pressing the “export as xyz”
button on the GSAS-II window.
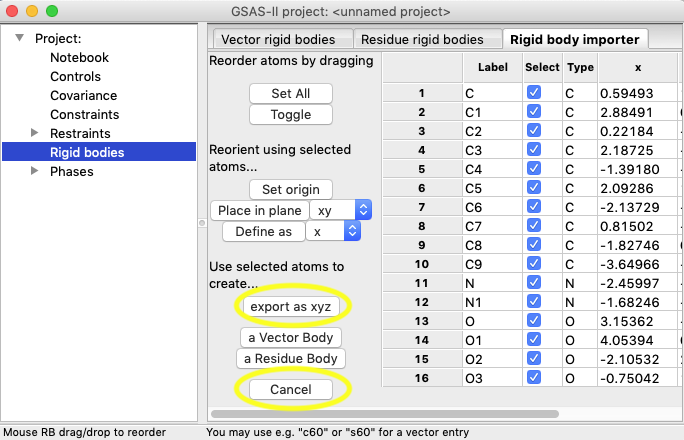
Make a note of the
file name, as it will be needed in the next step. Press Cancel to close
this window. It is fine to close GSAS-II, but it can also remain open.
Step 2: Regularize coordinates in Avogadro
For this step, it
is assumed that the cross-platform software Avogadro
program has been installed. If you do not want to install this program,
this step can be skipped, as described at the beginning of
Step 3.
2A) Read the coordinates into Avogadro by
starting the program and using the Avogadro File/Open command; select
the XYZ file type option and read the file produced in step 1D.
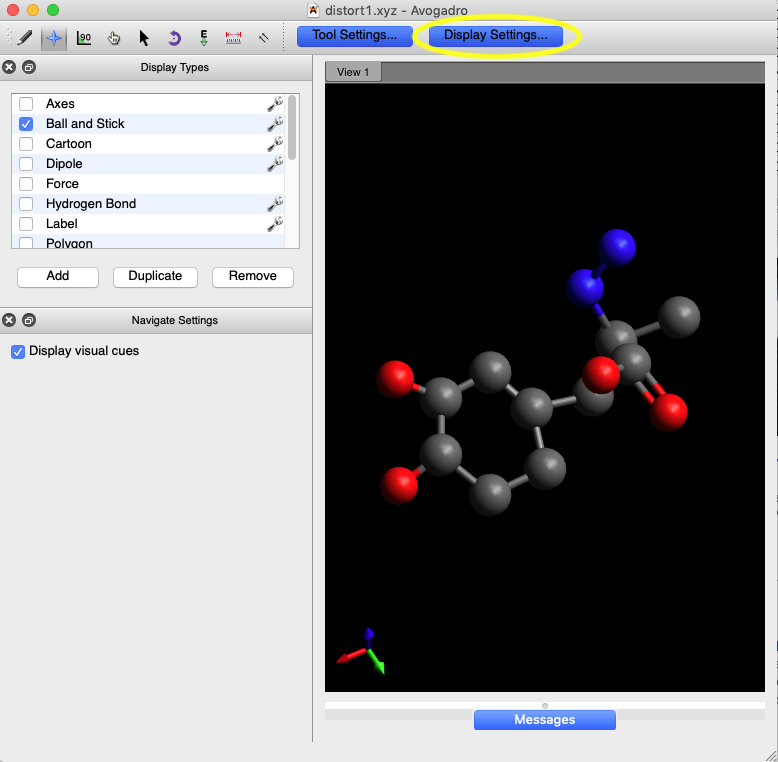
2B) Note that the program noted the correct
bonding of the carboxylic acid group, where one of the C-O bonds is noted as a
double bond, but the phenyl group does not have alternating double bonds. To
fix this, we need to click on the bonds, but that is difficult to do unless the
atoms are drawn smaller. Make sure that the Display Settings button is
selected (at top of window) and click on the wrench symbol to bring up
the “Ball and Sticks Settings” dialog, below.
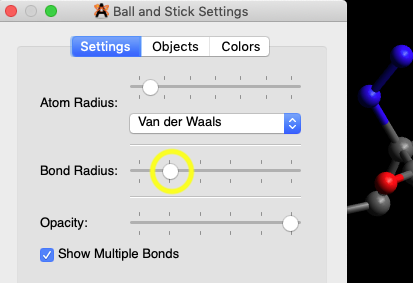
When the “balls” are
made smaller by moving the Bond Radius slider to the left, it
becomes possible to click on bonds.
2C) Switch to the
pencil in the toolbar
Click on directly on
every other C-C bond in the phenyl ring to change the bonds from single
to double. Note that when a C-C bond is clicked on, the order changes
successively from single to double and to triple and then back to single again.
(Use care to avoid clicking elsewhere than on a bond or additional atoms will
be created; use a right click to delete unneeded atoms.)
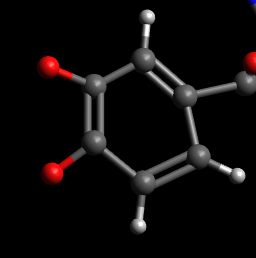
2D) Use the Build/“Add
Hydrogens” menu item to add the remaining H atoms to the other end of the
molecule.
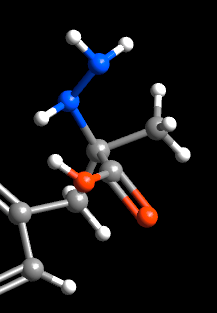
2E) Optimize the bond distances and angles using Extensions/“Optimize Geometry”. Use it a few times until no
further changes are visible. The molecule should appear as below, with
regularized bond distances and angles.
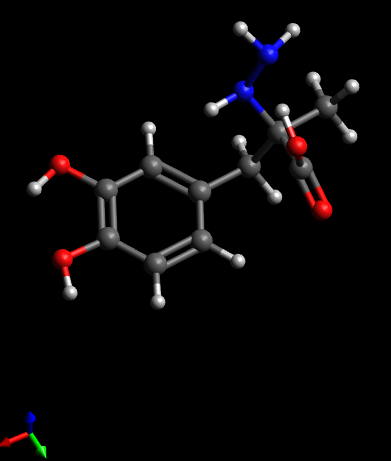
2F) Use “Save as” to write the newly
generated coordinates out. Be sure to select the file type as “XYZ”. I
used the name regularized.xyz
for the file. Exit Avogadro.
Step 3: Create the rigid body in GSAS-II
If you skipped
step 2, you can use the file I created with Avogadro, supplied as regularized.xyz in the Exercise files.
3A) To start, in GSAS-II open the distort1.gpx
file that is supplied in the Exercise
files. We then will create a rigid body for this
project. Start by clicking on the “Rigid bodies” tree item. Click on the
“Edit Residue Body”/“Extract from file” menu
item, select the format as XYZ and then select the file written in step
2F (regularized.xyz).
Note that the “Import XYZ” menu command could also be used, but “Extract
from file” allows atoms to be selected, recomputes the origin as the
midpoint between atoms and allows rigid body axes and the origin to be defined
based on user preferences. With “Import XYZ” the coordinates would be
used exactly as in created by Avogadro.
3B) After the regularized.xyz file is opened
and read; all atoms are selected by default. Note that H atoms are not moved
when torsional groups are rotated, so we do not want to include any of the
non-phenyl H atoms. For simplicity, here we will remove all of the H atoms.
(They could be regenerated later, if desired). Select only atoms #0-#15
(as below) and press Continue.
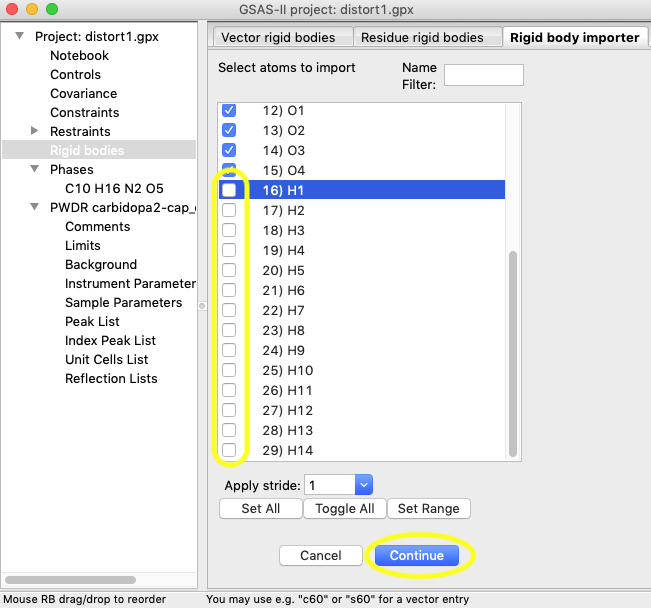
3C) Note that there are several other things that can be done on the
window that is now created. These include: defining axes and reordering the
atoms by dragging rows in the list. As an example, selecting the atoms in the
phenyl ring and pressing “Place in plane”, where the adjacent button has “xy” selected, will orient the z axis as normal to the plane
of the ring. Selecting a single atom and pressing “Set origin” will place that
atom as the origin, or if two atoms are selected the origin will be the
midpoint between the two atoms. None of this is needed here, but such actions
will likely be needed for bodies that will be placed at high-symmetry locations
in a unit cell.
For this exercise all that is needed
to select all atoms (done by default) and then use the selected atoms to create
a rigid body by pressing the “a Residue Body” button near the bottom of
the list of buttons.
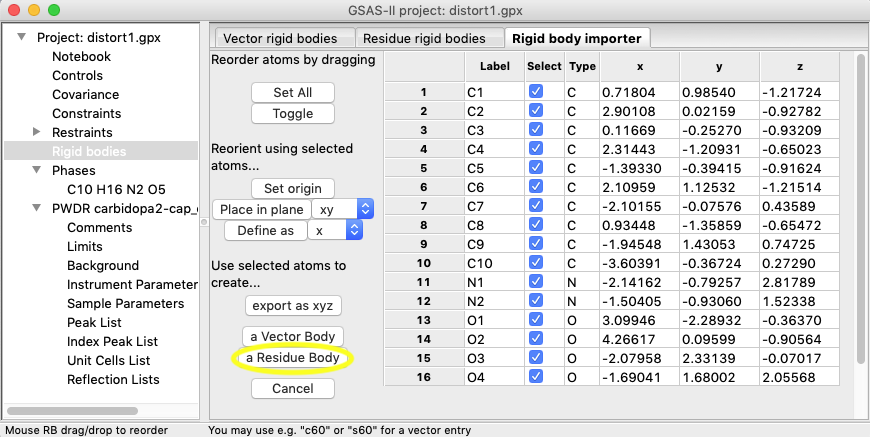
The rigid body is then created as
shown below.
3D) Find atoms in torsions
Press the Plot button to see the rigid body. Note that dragging with the left mouse
button held down is needed to see all the atom labels, as below.
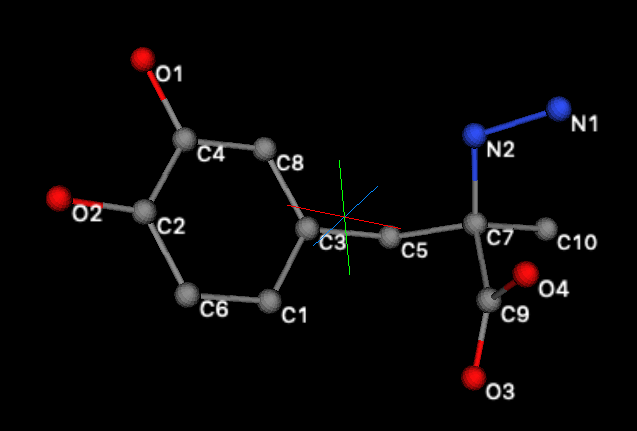
From this it can be seen that the four
bonds with possible torsional rotations are:
a)
C3-C5,
b)
C5-C7,
c)
C7-N2 and
d)
C7-C9.
3E) Define the torsions
Press the “Edit Residue Body”/”Define torsion” menu item. This opens a window to
select an origin atom. Once that is selected, you are offered a choice of atoms
that are bonded to the selected atom. Thus, for the C3-C5 bond, select C3
first to be the origin atom and press OK. This will
open a second menu with options for the pivot atom: C1, C5 or C8. Select C5.
(Note that if C5 had been selected first as origin, then the pivot choices
would be C3 and C7.)
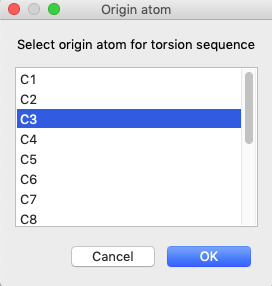
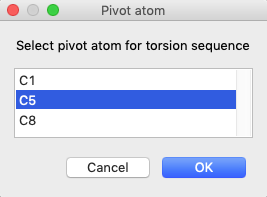
After defining the C3-C5 for a
torsion, repeat this to define a total of 4 torsions, by adding C5-C7,
C7-N2 and C7-C9. The torsions are displayed at the bottom of the
window, as shown below:
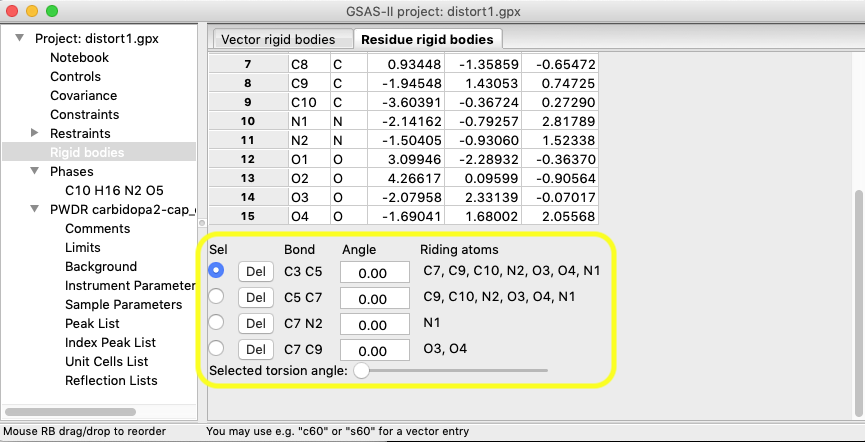
It can be instructive to select each
torsional mode in turn and move the slider to see how the mode rotates the
riding atoms.
Introduction to Steps 4 & 5
Now that the rigid body
has been defined, the next step is to insert it into the crystal structure
model. This means defining where the rigid body is located, oriented and how it
is mapped to atoms in the asymmetric unit. The origin of the rigid body
Cartesian system is placed at a specified location (in fractional coordinates)
and a quaternion defines the rigid body orientation. The same rigid body may be
inserted multiple times in the asymmetric unit. Each insertion of each body will
have a corresponding set of atoms in the asymmetric unit, an origin, a
quaternion for orientation. There will also be a set of torsion angle values
associated with each body insertion.
Note that
understanding GSAS-II’s 3D visualization system is key to managing rigid
bodies. It is valuable to move and rotate the representation, so that distances
along all axes can be visualized. For this it is valuable to understand that as
the structure is viewed, movement of the mouse while holding down a button
(also called dragging) changes the view of the crystal structure, as described
here:
· Dragging with the right
button down: moves the viewpoint, which is kept at the center of the screen
(effectively translating the structure).
· Dragging with the left
button down: rotates axes around screen x & y. Rotation is around the
viewpoint.
· Dragging with the center
button down: rotates axes around screen z.
· Rotating the scroll
wheel: changes “camera position” (zoom in/out).
Note that the screen axes are x: horizontal; y: vertical; and z: out of
screen. Also, there are additional plot controls available by pressing on the
“Draw Options” tab.
When inserting a
rigid body into a unit cell, as described in the next section, as the rigid
body is being located into the unit cell, a second set of actions can be
accessed with the mouse that affect the rigid body positioning. This is done by
holding the Alt keyboard key down while “dragging” the mouse.
· Alt+right mouse dragging moves the rigid body by shifting
the origin.
· Alt+middle button dragging rotates the rigid body
around the screen z axis.
· Alt+left button dragging rotates the body around the
x & y screen axes.
Visually, the rigid body motions are analogous to what appears when the
view of the structure is changed.
In this tutorial,
we want to place the rigid bodies into the approximate locations where those
molecules are already found. There are two ways to do this. One is that if
specified atoms in the rigid body are paired to atoms in the crystal, the
origin and/or quaternion can be optimized to best collocate those pairs of
atoms. This will be shown in Step 4. Another choice is to visually move the
rigid body to the desired location, which will be shown in Step 5. That process
might be needed to insert a molecule into a specific region of a structure to
fill a void or to account for density in a Fourier map.
Step 4: Insert the first rigid body into the model
In this step we
will assign matching pairs of atoms between the rigid body and the crystal
asymmetric unit and use them to determine the rigid body location.
4A) To start the
process of inserting a rigid body into a structure, select the desired phase in
the data tree (here there is only one choice) and then select the “Edit
Body”/“Locate & Insert Rigid Body” menu item.
If more than one body were defined, a window to select which body would be
offered. A farily complex window is displayed with
options to define where the rigid body will be placed, as below.
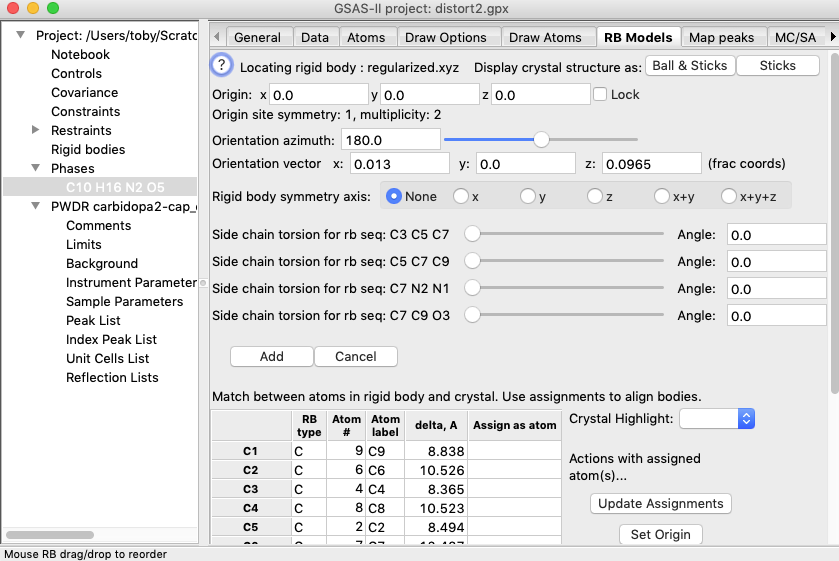
Also shown in the
GSAS-II graphics window is a plot of the structure, along with the rigid body
location. The structure will be plotted as was set in the Draw Atoms tab. Note
that here, by default, the asymmetric unit is shown with van der Waals spheres.
The rigid body is always displayed as a ball-and-stick model with green bonds.
Note that the origin of the rigid body is shown with a triplet of red, green
and blue lines (for x, y, & z, respectively). A white line is also shown that
displays the orientation vector. The red, green and blue lines (for x, y, &
z, respectively) of the unit cell outline show the origin and axes of the
crystal. The same color sequence show these axes on the
viewpoint.
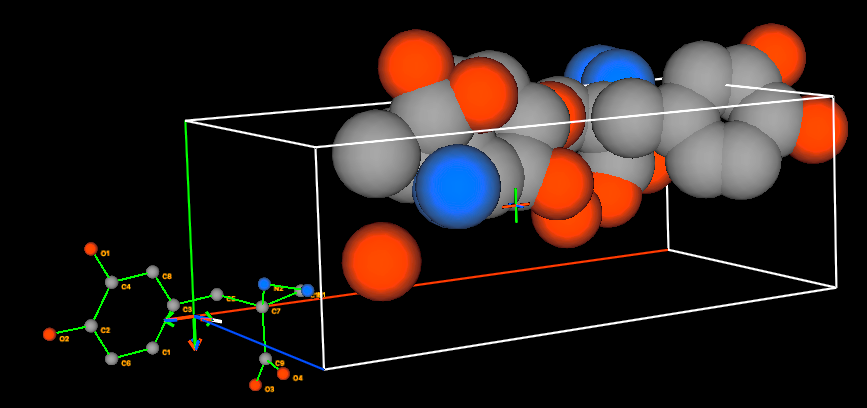
Change the crystal
structure display mode to either Ball & Sticks or Sticks (your
preference) using the buttons on the upper right. This is needed because with
van der Waals spheres, it is hard to see when the rigid body is close to the
location where it will be docked.
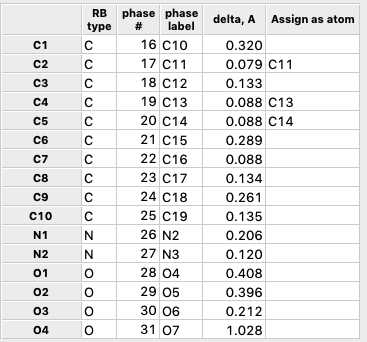
Note that the
table at the lower part of the window (as seen below) shows each atom in the
rigid body and the closest atom in the crystal structure as well as the
distance to that atom. In the column labeled as “Assign as atom” to the extreme
right of the table, we can assign specific pairing between atoms in the rigid
body and atoms in the crystal structure that will override the closest atom
pairing. As the rigid body is moved, the distances will be updated. Unless a pairing assignment has been made, the closest atom pairing
may change as the body moves.
4B) We will align the rigid body to the molecule
in the cell closest to the upper right corner by assigning rigid body atoms to
the matching atoms in the unit cell. Scrolling or expanding the window so
the entire table is visible will make subsequent steps easier
If we click on
the 2nd row in the table (with row label “C2”), the row is
highlighted.
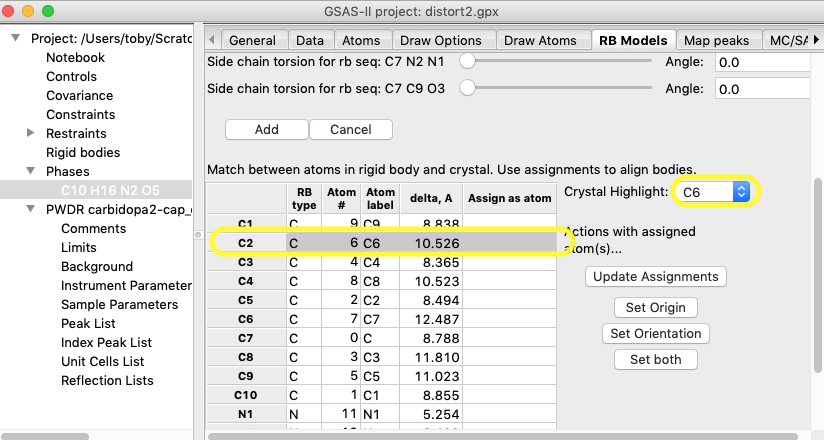
Note that atom C2 in
the rigid body is highlighted by the ball color changing to green, as well as its
paired atom in the crystal structure (C6), as shown below.
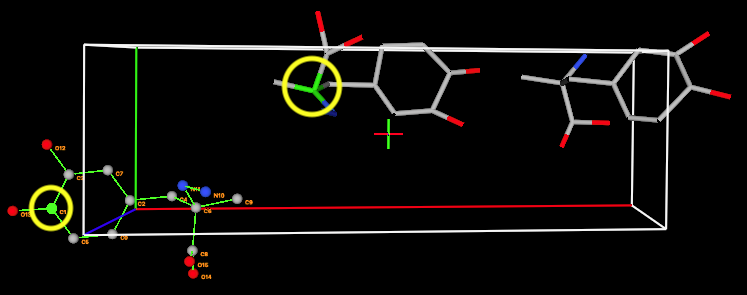
The crystal
structure atom is not the correct one to match to C2. To find the right one, we
can highlight different atoms in the crystal structure by pressing the Tab
keyboard key until the correct atom is displayed; alternately, select different
atoms in the “Crystal Highlight” pull down. After cycling through, one can see
that C11 in the crystal structure should be paired to C2 in the rigid body.
4C) Assign C11 in
the crystal structure to be paired to C2 by clicking in the right-most box in
the C2 row of the table and selecting atom C11 from the dropdown list,
as seen below.
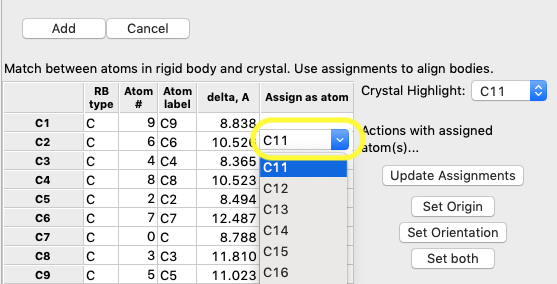
Optional: press “Update
Assignments” button and the distance between RB C2 and unit cell C11 will be
shown in the table. Likewise, pressing “Set Origin” will translate the rigid
body to best match the assigned atoms. Since there is only one assigned atom,
the distance will be zero.
4D) Setting the orientation and origin requires
assignment of at least two more atoms and preferably more. Select another easy
to identify an atom in the rigid body by clicking on the C4 row in
the table. (Alternately, press Alt-Tab to highlight different rigid body
atoms.) Using Tab, it can be seen that crystal structure atom C13 should be
paired to RB atoms C4. Select atom C13 in the “Assign as atom” cell for
C4.
Likewise, rigid body
atom C5 should be assigned to crystal structure atom C14 by selecting atom
C14 in the “Assign as atom” cell for C5.
4E) Then press
the “Set Both” button and the phenyl ring positions are approximately
matched, as below.
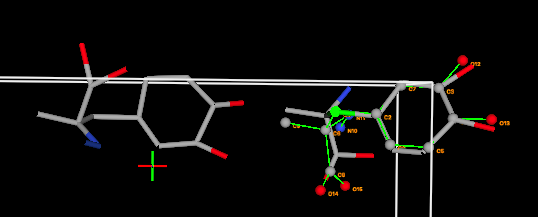
4F) The agreement in atom positions at the other
end of the molecule is still not very good, and this can be improved by repositioning
the view (dragging with the left mouse button) to look approximately along
the plane of the ring. When this is done, it becomes clear that the agreement
can be improved significantly by rotating around the first torsion angle
by moving the slider. An angle of ~23 degrees brings the atoms much
closer, but there are still atoms as much as 1 Å in disagreement, since the molecule
in the crystal structure is rather distorted.
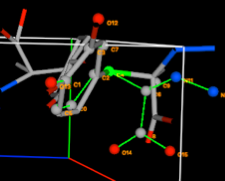
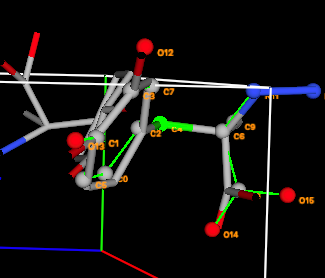
4G) Note that the
table now shows that the rigid body has crystal structure atoms 16-31 paired.
The pairing is consecutive, which is to be expected since the ordering of atoms
was never changed, but this is not required.
Press Add to insert the rigid body, using the parameters shown in
the window. A warning is displayed, since some of the distances are larger than
0.5 Å, but press Yes since this is about as good as we can do.
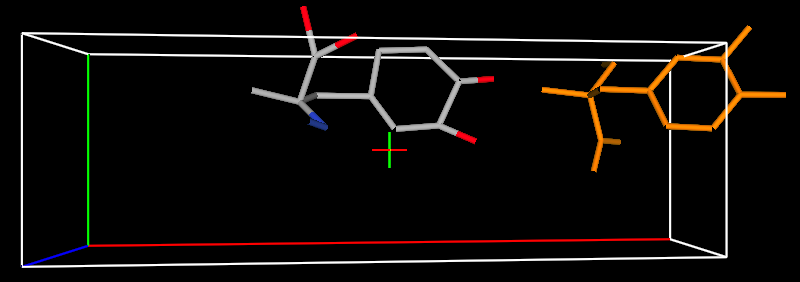
Pressing Add causes any
unpaired (shown as “create new”) to be added to the Atoms list and then every
atom in the rigid body is linked to an atom in the asymmetric unit. The rigid-body constrained atoms are now
shown with bonds in orange (unless “Show Rigid Bodies” is unchecked on the
“Draw Options” tab.) The atom coordinates are shown with a grey background on
the Atoms tab. Press the c key (with the graphics window active) to see the
view below.
Step 5: Insert the second rigid body into the model
As mentioned in
the introduction to steps 4 & 5, above, holding a mouse button down (mouse
dragging) changes the view of the crystal while holding Alt down while dragging
the mouse, repositions the rigid body within the cell. In this step, to show
how that works, we will use the mouse to place the rigid body.
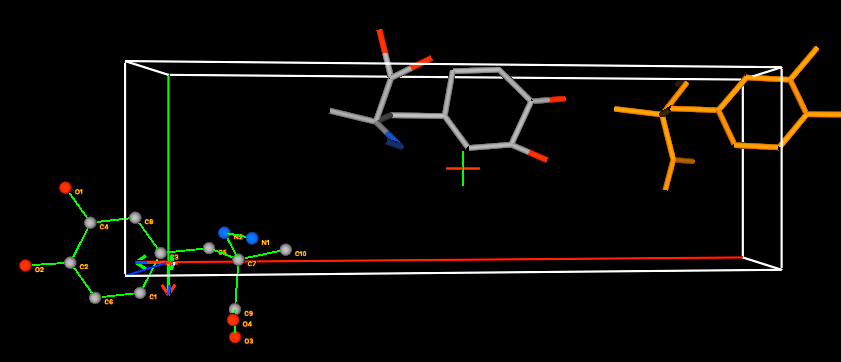
5A) To insert the rigid body into the structure
again to match the second copy of the molecule, again select the “Edit Body”/“Locate & Insert Rigid Body” menu item. A window is
displayed as before with options to define where the rigid body will be placed.
The graphical display will look like this:
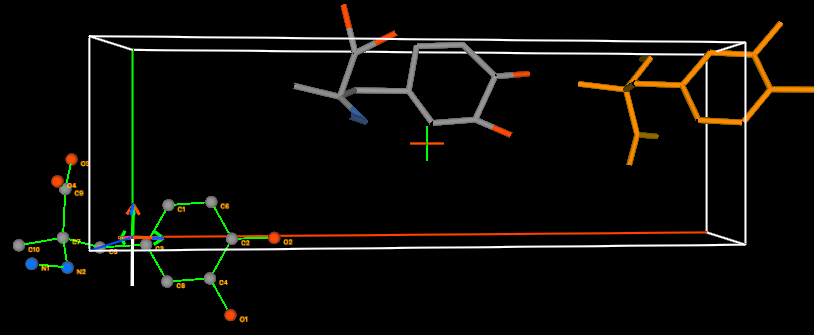
5B) Hold the Alt
key down and drag with the middle mouse button to rotate the
rigid body by 180 degrees, as shown below.
5C) Again with the Alt key down, drag with
the right mouse button and move the rigid body so that the phenyl rings
are more or less aligned.
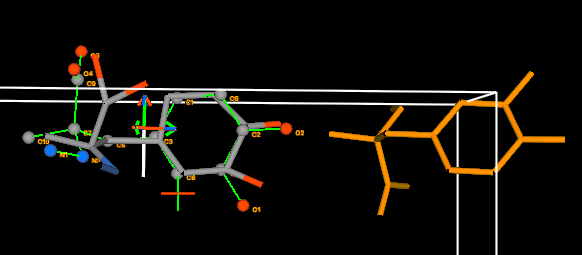
5D) To see how far the rings are separated in the
screen z direction, we must rotate the view. Drag the mouse upwards
with the left button down (without pressing Alt) to obtain a view
similar to the one below.
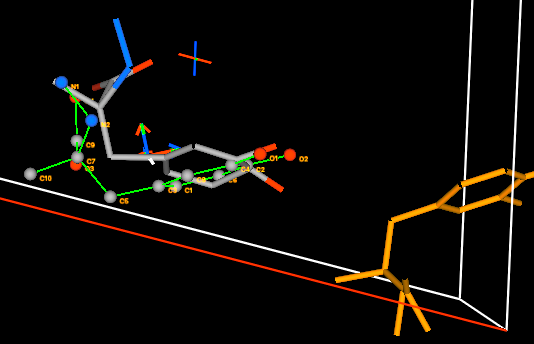
From this view it is
clear that both a small rotation and a small translation is needed. First with
the Alt and the middle mouse button both pressed, drag upwards
until the two rings molecules are more parallel. Then, with the Alt and
the right mouse buttons both pressed, drag upwards until the molecules
are better overlapped.
5E) At the point
the rigid body is pretty close to the position of the molecule in the unit
cell, with distances in the table ranging from 0.1 to nearly 2 Å, but better
agreement can be obtained by making small adjustments with the Alt down and
successively pressing each of the three mouse buttons alternated with changing
the view to see the molecules from a different perspective. Another choice is
to assign several atoms and optimize, as was done in steps 4D and 4E. Choices
of atoms to optimize are clear, since the atoms are properly paired in the
table. Updating the C3-C5 torsion to ~20 degrees will also improve the
agreement.
5F) When the
agreement is sufficient, press Add, accept the warning and this molecule is
also now constrained by the rigid body. Now both molecules will appear as
orange.
Step 6: Optimize the model
If the number of
cycles is set to zero (in the Controls tree item), the fit will be seen to have
gotten significantly worse, with the profile wR
jumping from 2.2% with the distorted model to ~6%. This is not surprising and
only a few refinement steps will provide a more realistic model with comparable
agreement, but far fewer parameters.
6A) Initially, turn off refinement of all
atoms. (Select the Atoms tab, double-click on the refine column
label and then leave all boxes unchecked and press OK). Note that the X flag
for the atoms in the rigid bodies would be ignored anyway.
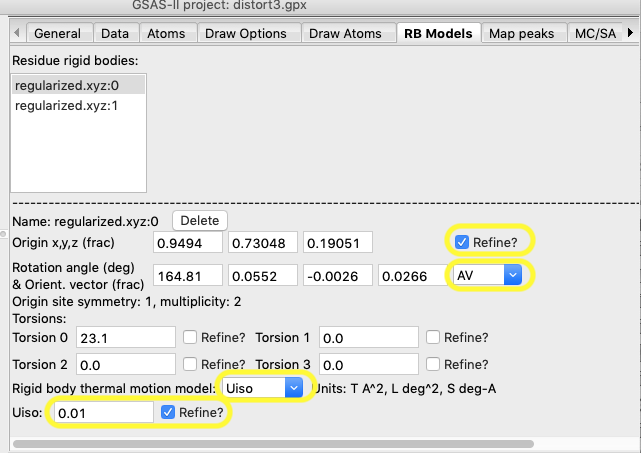
Then select the RB
Models tab. The first rigid body is automatically selected. Make the
following changes:
1.
Select to refine the Origin
2.
Refine both the orientation azimuth and vector by setting the AV
flag
3.
Set the “thermal motion” mode to Uiso
4.
Set the initial Uiso value to
something reasonable, say 0.01
5.
Set the refinement flag for thermal motion
6B) Then select the second rigid body and repeat
the previous actions (setting the refine checkbox, selecting AV
for the orientation refinement, setting Uiso
mode, set the Uiso value to 0.01
and set the thermal motion refinement flag.)
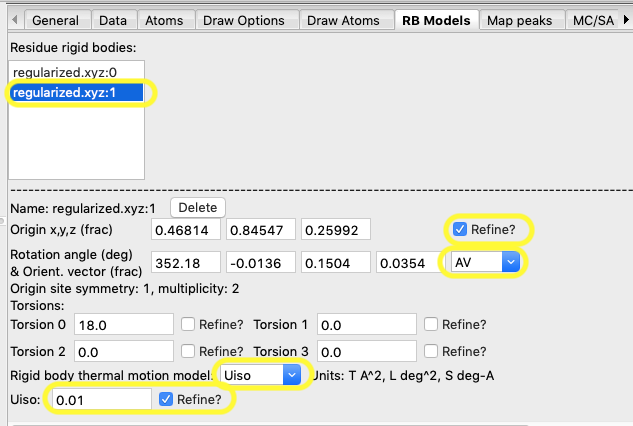
6C) Set the number of cycles back to 5 and
refine. The fit will converge quickly to an wR
of ~4%.
6D) Add
refinement of the four torsion angles for each of the two rigid
bodies. Then refine again. The wR quickly drops
to 2.5%
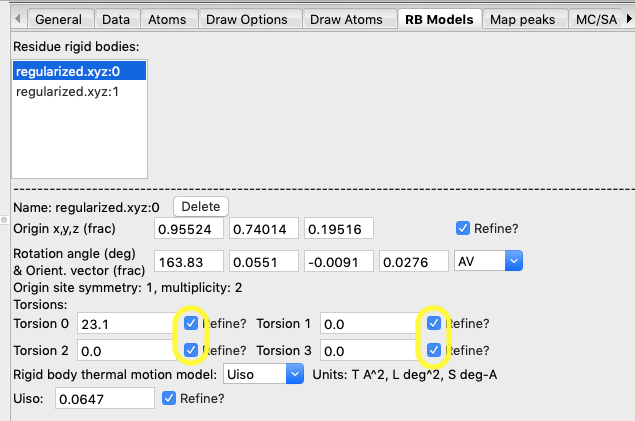
Optional Step 7: Try rigid body TLS motion
The motion of
rigid bodies, known as the TLS description, has been worked out (Schomaker & Trueblood, Acta Cryst.
B24, 63-76, 1968) and consists of three tensors:
·
the T tensor for translation movement of all atoms together
·
the L tensor for libration, rotation of all
atoms as a unit around the rigid body origin, and
·
the S tensor, to describe correlated librational-translational
motion (screw-like motion). The S terms can be readily omitted if the rigid
body origin is at the body center of mass.
In the full expansion there are 6 T and 6 L and 8 S terms. It is
unlikely that all of these terms can ever be used with a powder dataset.
The simplest
description that can be made with a rigid body is to assume that all motion is
translational and isotropic. This is what we have done previously and is
equivalent to refining Uiso for each atom in the
rigid body, but applying a constraint so that all atoms in the rigid body share
that Uiso value. It makes sense to see if further
expansion of the rigid body motion/disorder description will produce an even
better fit, although it is clear that the crystallographic fit is already quite
good considering the limited resolution and high background levels. Refining 24
more parameters (6 T + 6 L, for each of the 2 bodies) is clearly impractical.
One possible simplification would be to refine only the diagonal T & L
elements (which constraints translation and libration
directions to crystal axes). That might be appropriate with data more sensitive
to group motion, but is still impractical here. One still simpler model is to
include translation and libration, but require equal
amplitudes in all directions. This can be done by refining only the diagonal T
and L terms, but to constrain them to be equal. If the T & L values are
constrained to be the same for the two rigid body insertions, this means
replacing the 2 grouped Uiso values with 2 terms (a
single Tjj and a Ljj
term applied to all rigid body atoms). This is easily done as shown below.
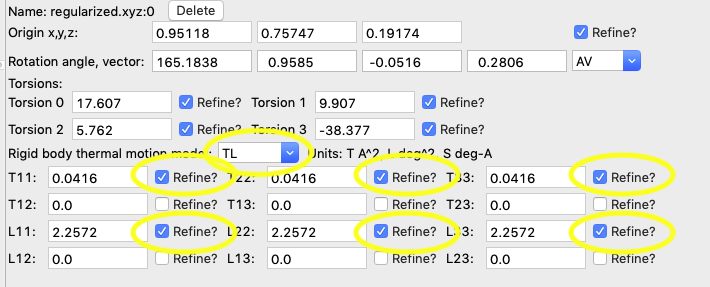
7A) Switch to
refine the T & L terms by selecting each body, in the RB Models
phase tab, set the thermal motion model to TL for both rigid bodies and
then turn on the refine checkbox for the T11, T22, T33, L11,
L22 & L33 terms.
7B) Delete the two
existing constraints on Uiso
values: Use the Constraints tree item and the Phase tab and delete
the two entries. These constraints are actually ignored when rigid body
group motion is refined, so the presence of these constraints does not actually
have any effect, but it is better to remove any unused constraints.
7C) Create constraints on the Tjj
and Ljj terms through use of the Constraints
tree item. To constrain the Tjj terms, one
needs to know their variable names are RBRTjj:b:0 for body #b of type 0
where j = 1, 2 or 3.
On the Phase tab
(loaded by default), use the “Edit Constr.”/“Add
Equivalence” menu item and enter RBRT in the search filter.
The first term is one of the six that needs to be constrained, so select it as
the 1st variable and press OK.
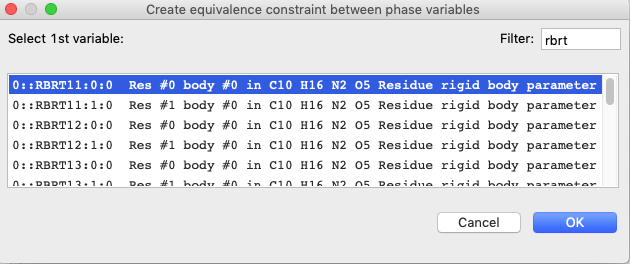
On the next window
select the remaining five 11, 22 and 33 terms
and press OK:
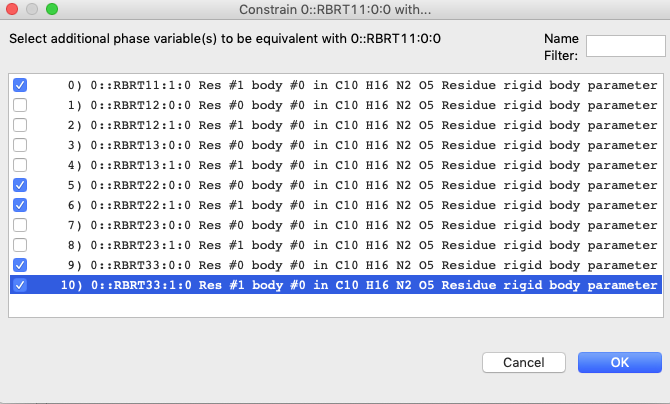
7D) Create constraints on the Ljj
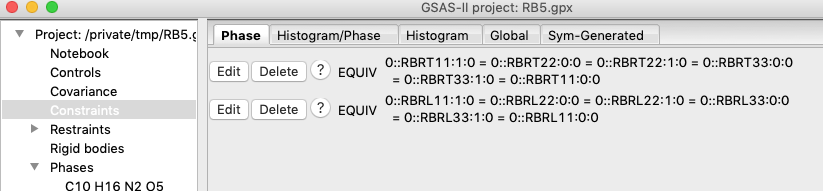
terms through use of the Constraints tree item as was done before. Their
variable name is RBRLjj:b:0. Again use the “Edit
Constr.”/“Add Equivalence” menu item and enter RBRL in the search filter.
The first term is one of the six that needs to be constrained, and on the next
screen select the remaining five 11, 22 and 33 terms and press OK. Constraints
should appear as:
7E) Then refine with these parameters and
the Rwp remains at 2.5%, but I would argue this is a
more reasonable model than the Uiso model. If the
thermal ellipsoids are plotted, they get larger further away from the origin as
one might expect.
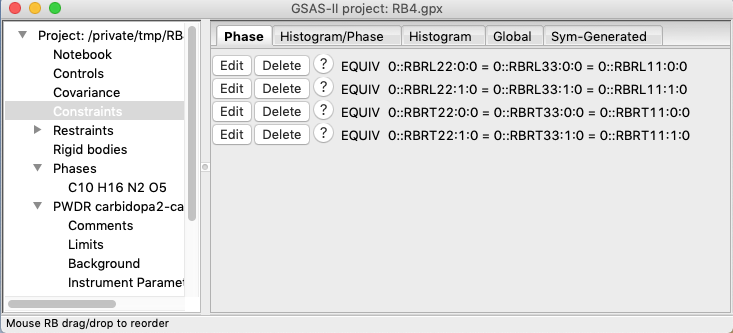
7F) An even
more relaxed model would be to allow the Tjj
and Ljj terms to differ between the two
bodies, with constraints as shown below, but this produces no improvement in
the Rwp. Further it has a non-physical negative Ljj value for one of the two bodies, so this is
not a better model.
Conclusion
In this tutorial, we have seen how to create a rigid body, using the Avogadro program to regularize the internal geometry. The body was then imported into GSAS-II, including 4 torsion angles internal to the body. The rigid body was then placed into the unit cell in previously determined positions/orientations. The positions, orientations and torsions, as well as rigid body group motion parameters, were then refined. The resulting fit was excellent, with a highly realistic structure and a small number of parameters that are appropriate for the dataset being used.