Create Instrument Parameter File: Determine Starting Profile from a
Standard
The goal of this exercise is
to determine approximate instrument profile parameters by a quick peak fit to a
sample with a lab diffractometer. Then in step 3.4 a new instrument
parameter file is created allowing these parameters to be used as
the starting point with other datasets.
Ideally, one should use a material or mixture
of materials that has peaks over the entire range where you collect data and
use a material(s) that have negligible sample broadening (from crystallite size
or microstrain). The NIST LaB6 standards
(SRM 660, 660a and 660b) are good choices for this, as they have very little
sample broadening and a relatively small number of peaks but over a wide angular
range, although it would be good to have peaks starting somewhat lower in
2theta.
Note that it
is highly recommended to collect reference data to a much higher 2theta angle
than here. What is done in this part serves as an example, and is sufficient
only if one will never collect and use data above 70 degrees (unlikely!).
To get started, create a new
project in GSAS-II, either by starting the program fresh or using File/New Project.
Step
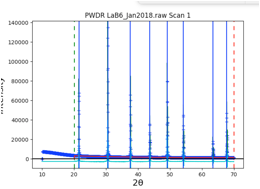
1: Read in the Diffraction Data
Use
Import/Powder Data/from Bruker RAW file to read file LaB6_Jan2018.raw from the Tutorials CWInstDemo/data
directory (download from https://advancedphotonsource.github.io/GSAS-II-tutorials/CWInstDemo/data/).
After selecting this file, answer yes to "Is this the file you want?"
Step
2: Select Default Instrument Parameters
The next dialog to appear is
titled, "Choose inst. Param file for
LaB6_Jan2018.raw Scan 1 (or Cancel for default)" since we do not have a
set of parameters to read, we must use a default set. Press Cancel.
This raises the default inst parms dialog, as below
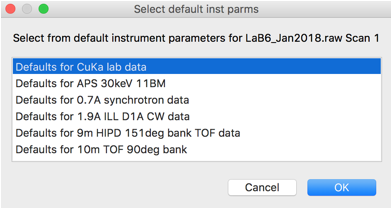
Here, choose the first option for CuKa lab data
(which is for a standard instrument with Kalpha1 and Kalpha2 radiation) and press OK. A plot of the data will
appear as below.

Step
3: Change Data Range.
Note that the data begins at
10 degrees, but the first peak is above 21 degrees, we can simplify the
background fitting by changing the data limits. Click on the Limits data tree item, and either change the Tmin value from 10 to 20 or in the plot "drag" the green line to the
right to approximately 20 degrees.
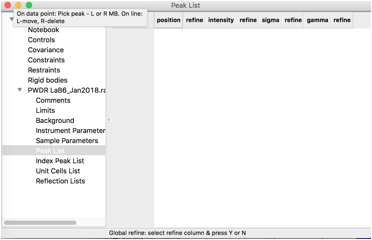
Step
4: Add Peaks to Fit
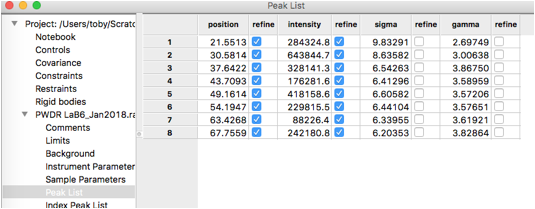
To define peaks, click on the "Peak List" data
tree item. Note that as below, the peak list is initially empty.
Move the
mouse to any of the data points close to the top of the first peak and click the left mouse button. A line will be
drawn through the peak and the position will be added to the peak table and a
line marking this is added to the plot, as below.

Repeat this for all 8 peaks in the pattern. Note that if a peak is entered in the
wrong place it can be moved by "dragging" it with
the mouse, or use a right-click to delete it. Be careful to make sure
two peaks are not entered in the same place by accident.

The peak table appears as:
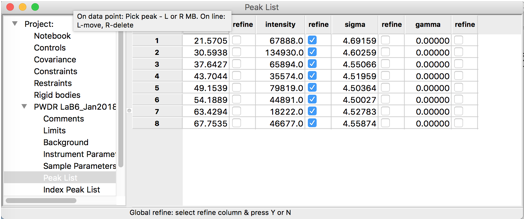
Step
5: Refine Peak Areas
By default, the peak
intensities are flagged as to be varied, but not any
of the other parameters. It is wise to refine them all, but we want to make
sure the parameters have a chance to converge one step at a time and we should
start with only the intensities.
Use the Peak Fitting/Peakfit menu item to perform a peak refinement. You
will be asked for a name to save the project (enter a name such as peakfit.gpx and press Save). The peaks are then fit, here
optimizing only the intensity values. The console window shows the details of
the refinement:
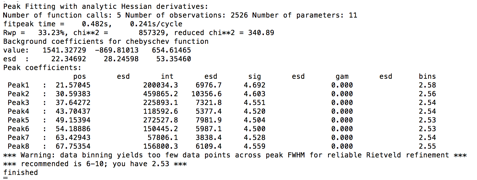
The warning at the end is
because the default peak parameters describe a peak shape that is significantly
sharper than what is actually present for these data; the step size is actually
fine. This warning will later go away, but if it did not this would indicate
that it would be better to recollect the data with a step size decreased by a
factor of 3-4.
Step
6: Refine peak areas and heights
In the peak list window, double click in the refine heading for the
peak position flags, this will bring up a dialog
that allows all peak positions to be varied.

Select "vary all"
and press OK. Now all peak positions and areas will be refined.
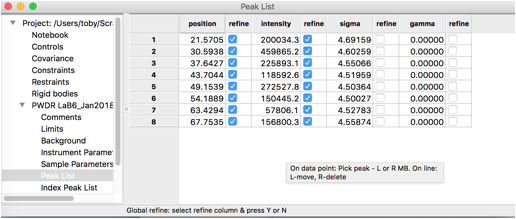
Use the Peak Fitting/Peakfit menu item to start
peak refinement.
The fit improves significantly,
as below, but further improvements are needed.
Step
7: Refine peak areas, heights and widths (optional)
Double-Click
on the refine headings for the sigma
(Gaussian width) and gamma
(Lorentzian width) parameters so that all parameters can be refined. Use the Peak Fitting/Peakfit
menu item to start peak refinement. The results in the console window are as
below. This is being done here just
to see how the individual peaks vary before we fit them with a parametric
equation. This step is not necessary, but provides a useful graphical reference
to look for any anomalous peaks that one might not want to use.
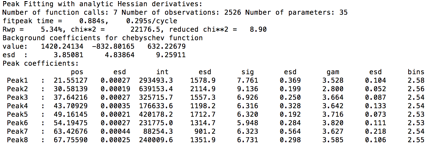
Step
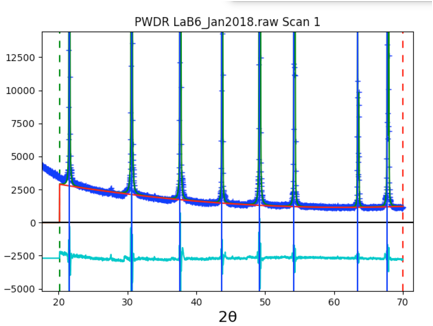
8: Add more Background terms
Use the zoom feature
(magnifying glass) to draw a box around the low intensity data

Looking at the plot (see
below), makes it clear that the background is not well
fit. Adding more background terms will fix this.
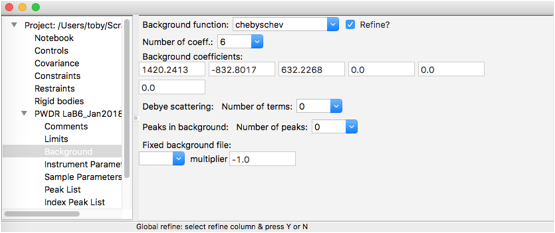
Select the Background tree item and change the number of coefficients to 6, as shown
below.
Then return to the Peak List data tree item and use the Peak Fitting/Peakfit
menu item to perform a peak refinement. At this point it is instructive to
click on the Instrument Parameters
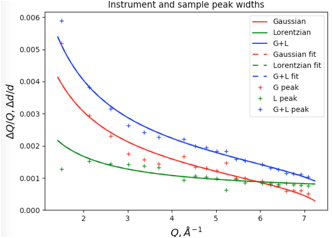
data tree item to see a plot of peak widths:
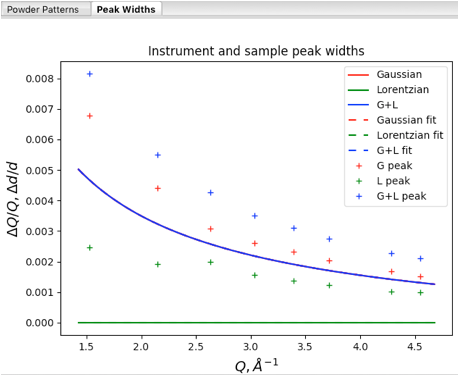
Note that the solid curves
here are plots of the profile coefficients from the default instrument
parameters (which are unimportant here), but the fits for the individual peaks
are shown (in units of Q/delta-Q vs Q), with
Lorentzian widths (gamma) in green, Gaussian widths (sigma) in red and their
convolution (total broadening) in blue.
Step
9: Refine Profile Parameters
Now, select the profile terms
to be refined. Use Gaussian U, V, & W and Lorentzian X
& Y (note that Z, which provides constant broadening, independent of Q,
is provided as an option, but is rarely if ever needed.)

Note that these U, V & W
values will be used to set the Gaussian peak widths for those peaks where sigma
is not being refined and likewise X, Y & Z will be used to determine the Lorentzian
widths where gamma is not refined for that peak. If we had any peaks that were
not consistent with the width of the others, we might choose to continue to
refine their individual profile terms (sigma & gamma), if that is done the
peaks varied individually would be excluded from the U, V, W, X & Y
refinements. Here we will refine U, V, W, X & Y against all peaks. To do
this, select the Peak List data tree
item and remove refinement of sigma
& gamma for all peaks by double-clicking on the refine column headers
for each and select "N – vary none" so that the table appears
as below:
Use the Peak Fitting/Peakfit menu item to perform
a peak refinement optimizing U, V, W, X & Y:

Note that the sigma and gamma
values are now computed from U, V, & W and X & Y, respectively. The
difference curve shows very small deviations.
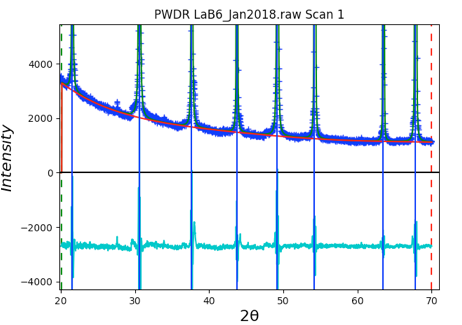
Note that the background is
also quite well fit now.
Step
10: Save the Profile Parameters
So that we can use these
profile terms as the starting point for a future refinement, save the profile terms to a file by
clicking on the Instrumental Parameters
data tree item and use the Operations/Save
Profile menu command. Give the file a name that will be helpful for future
use (<MyInstrument>20-70deg.instparm might be good) and
put this file in the directory(s) where you will keep your data files.
Clicking on the Instrument
Parameters data tree item will show the peak widths from U, V, W, X & Y,
and also the individual peak widths generated from those values (not very
useful). For a more useful plot we refining the individual peak widths
independently again, as shown in the next section.
Step
11: Plot Profile Parameters with Individual Peak Widths (optional)
First we stop refining U, V, W, X & Y by
clicking on Instrumental Parameters
data tree item and turning the refinement flags off.

In the Peak List data tree item, turn on refinement of all
individual peak widths (as we did in Step 7)
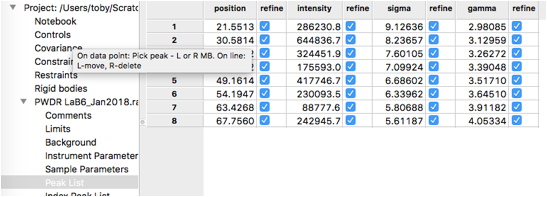
and use the Peak
Fitting/Peakfit menu item to perform a peak
refinement optimizing individual peak widths, as before. Returning to the Instrumental Parameters data tree item
provides this plot:
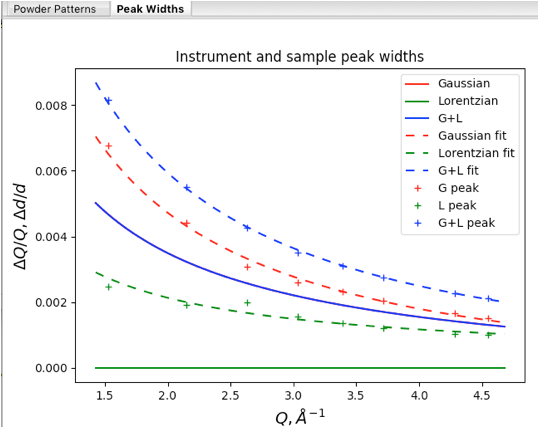
The displayed lines and
points are as follows, where Lorentzian widths are shown in green, Gaussian
widths are in red and their convolution (total broadening) is shown in blue:
á Solid curves: profile terms from original instrument parameter
file (here the CuKa lab data defaults). Note since X,
Y & Z are zero, there is only Gaussian broadening and the total broadening
is exactly the same as the Gaussian so the blue curve hides the red one.
á Dashed
curves: these
values are generated by U, V & W and X, Y & Z. Note that the broadening
from this instrument is significantly greater than the default values.
á Plus signs
(points): these are the widths for
the individual reflections unconstrained. Note that they agree well with the
fitted curves (dashed lines).
These profile terms are more than adequate for most
structural fitting problems, but it should be noted that these values are not sufficient
to obtain quantitative measurements of microstrain
and/or crystallite size. To obtain even better terms the instrument profile is
best determined by a Rietveld fit for (with a standard where microstrain and size are known to be negligible or at least
have certified values) Those certified values should be set as input values and
not refined to allow U, V, W, X, and Y to be further refined. Ideally, in
addition to higher angle data, the sample would also have lower angle peaks and
SH/L can also be refined.
Part 2: Test the Profile Parameters
The obvious question will be
how well do these parameters fit the data? To test this, we can start a new
refinement using these parameters and see how well they do.
Step
2.1: Read in the Diffraction Data
Use
File/New Project to create an empty project. You can say Yes
to the prompt to save the current project (No would not hurt.) As before, use Import/Powder Data/from Bruker RAW file to read file LaB6_Jan2018.raw from the Tutorials CWInstDemo/data
directory (downloaded already from https://advancedphotonsource.github.io/GSAS-II-tutorials/CWInstDemo/data/).
After selecting this file, answer yes to "Is this the file you want?"
Step
2.2: Select New Instrument Parameters
The next dialog to appear is
titled, "Choose inst. Param file for
LaB6_Jan2018.raw Scan 1 unlike before, we do have profile terms to read, from
the file created in Step 10, above. Select the file written before (such as
<MyInstrument>20-70deg.instparm
) and press OK. Note that you may need to change the
file filter to see files of type .instparm.
At present, the instrument
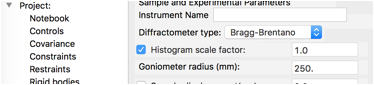
type is not saved, so go to the Sample Parameters data tree item for the new
histogram and change the Diffractometer
type from Debye-Scherrer to Bragg-Brentano.
(before)

(after)
Step
2.3: Add Phase
We will add a phase for LaB6, since this is a simple material we will input this by
hand rather than trying to import it. Use
Data/Add new phase to create a new phase. Enter any name you choose, though LaB6 is a good choice and press OK.
The symmetry and cell need to
be edited on the new phase's General tab. Click
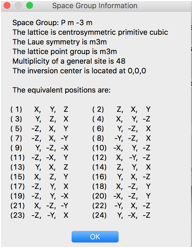
on the Space Group Button (which defaults to P1) and enter P m -3 m (note use of spaces to separate symmetry axes
– though in this case since this is a standard setting, omitting the
spaces works too. The space group symmetry information is
displayed, click
OK.
Change the lattice constant (a) from
1.0 to 4.15689 A. (The value for SRM
660b)

Finally add atoms to the
phase by clicking on the Atoms tab. Use the Edit Atoms/Append atom menu item to insert an atom. A new atom is
included in the table.

Double-Click
on the Type value (H) and which
opens a periodic table window. Click on the arrow next to La to bring up a menu of the defined valences

Select La
(neutral atoms are usually preferred) from that pull-down and the period table
window closes. This atom is located at position 0,0,0 so no further editing is
needed. For completeness add the second by using the Edit Atoms/Append atom menu item again. to
insert an atom. For the second atom, change the type to boron by Double-Clicking on the Type value (H) and selecting B (the
only choice) from the pull-down. The coordinates for this atom are
0.1975,0.5,0.5 so the x, y and z values must be edited.

Note that the site
multiplicities indicate that the stoichiometry is La1B6,
as is expected.
Step
2.4: Link Histogram and Phase
Click on the
Data tab for the phase. Note that
there are no associated histograms:
Use the Edit Phase/Add Powder Histogram menu command. Select the one histogram and press
OK.
Nothing needs to be changed
of the new parameters added here:

Step
2.5: Refine Histogram Parameters
We will first change a few
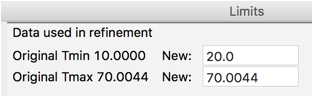
histogram parameters. For data tree item Limits
change Tmin to 20 degrees, as was done before in
step 3.
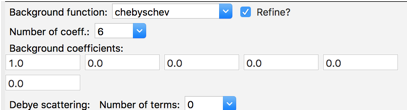
For data tree item Background change the Number of coeff. to 6, as was done before in step 8.
Note that the refinement flag
is on by default. We will not refine any of the Instrument parameters
but we will refine the histogram scale
factor (only) on the Sample
Parameters.

Use the Calculate/Refine menu item to start refinement. The program will prompt requesting a
name for the newly-created .gpx
file.
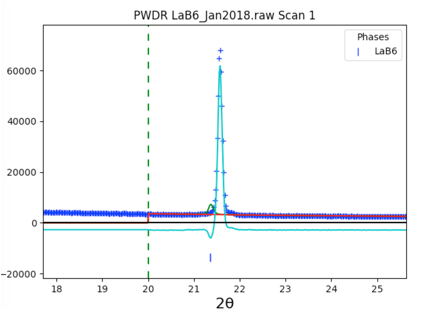
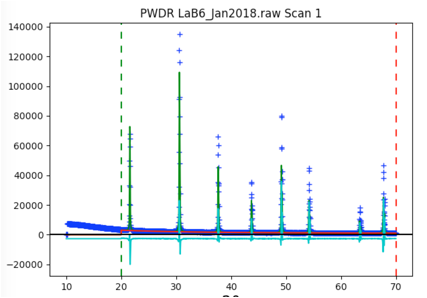
The fit is not very good. Clicking on the histogram's (PWDR) data tree item and zooming in
shows that the tick are not well aligned with the
peaks. This is due to sample displacement.
Step
2.6: Refine an additional Histogram Parameter
The position of the sample is
never well determined in a Bragg-Brentano instrument, so the sample
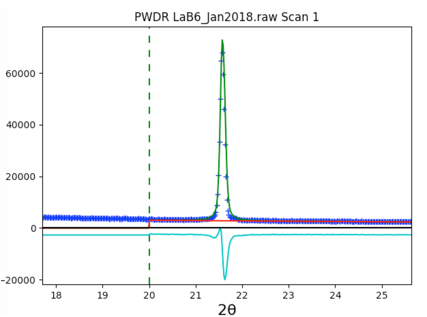
displacement should always be varied. Click on Sample Parameters and turn on refinement of Sample displacement.

Use the Calculate/Refine menu item to start another refinement. Significant improvement is seen and even
more if Calculate/Refine is used a
second time.
Step
2.6: Turn on Le Bail fitting
Part of the problem in the
fit is that the intensities are not well fit in the model. Rather than fitting
the few free structural parameters (x for B and Uiso
values), we will treat the intensities are arbitrary using Le Bail fitting. This is done by clicking on the Phase tree item and the Data
tab and setting the do LeBail
extraction flag.
Use the Calculate/Refine menu item to start another refinement. A warning message that "Steepest
Descents dominates" this is because a high degree of parameter correlation
occurs as the reflection intensities change. The fit does not improve very much
if Calculate/Refine is used a second
time but the warning goes away.
Step
2.7: Fit Lattice
While this should not be
needed for a standard, it is clear by looking at the plots that peaks are still
not quite line up. In a less dense sample it might be reasonable to refine the
sample transparency, but here the only reasonable parameter is to refine the
lattice. On the Phase's General tab press the Refine unit cell control.

Use the Calculate/Refine menu item to start another refinement and the
positioning of the peaks improves significantly.
Step
2.8: Fit MicroStrain
The remaining major problem
is that we have not treated the sample broadening and LaB6 does have some microstrain. That can be refined with the Phase's Data tab with the microstrain control.

Use the Calculate/Refine menu item to start another refinement. A second
refinement cycle brings the Rw to circa 5.8%. The fit
improves dramatically and microstrain refines to a
non-physical negative value. This is because our somewhat naive approach above
assumed no sample broadening.
This shows why if you are planning to measure microstrain and/or crystallite size quantitatively, you
should determine instrument profile using a Rietveld fit with a standard with
known values for the microstrain and size. Fix the
size and microstrain to the known values when fitting
the data from the standard.
Step
2.9: Additional Parameters
For these data, it appears
the ratio of Kalpha1 and Kalpha2 is not exactly the theoretical value of 0.5.
This can happen due to monochromator tuning. Allowing this to shift slightly by
including brings the Rw to circa 4.9%.
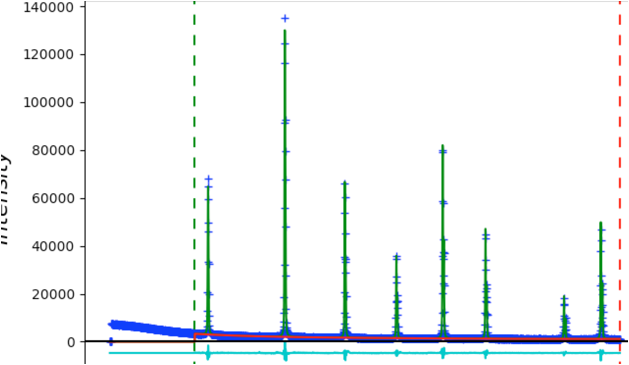
The fit is quite good without
fitting the instrumental profile terms:
Step
2.10: Profile Term Quality Check
The quality of the profile
parameters we previously fit can be demonstrated by turning off refinement of
the microstrain term and refining the U, V, W and X
& Y terms. This produces a small improvement in the fit (expected as one
fitting parameter as been replaced by 5), but the changes are very small, as
noted by the Instrument Parameter terms plot:

Part 3: Fitting data over a wider range
In this section we fit a
pattern with a wider range of data. This proceeds quite simply.
Step
3.1: Start new project and read in data
Restart GSAS-II or use the
File/New Project
to create a new empty project.
Use
Import/Powder Data/from GSAS powder data
file to read file
NIST660CBI.gsas from
the Tutorials CWInstDemo/data directory (download
from https://advancedphotonsource.github.io/GSAS-II-tutorials/CWInstDemo/data/).
After selecting this file, answer yes to "Is this the file you want?". As before, use Cancel to select the default CuKa lab data instrument parameters.
Step
3.2: Change Data Range
Since the background is quite
curved at lower angles, reducing the angular range to be fit will require fewer
background terms. Select Limits in the data tree and then set Tmin to 20.
Then select Background in the tree and change the number of background
parameters to 8.
Step
3.3: Add Peaks
Select Peak List from the
tree allows adding peaks. Zooming in on the lower portion of the pattern makes
it easier to see all the peaks. Be sure to click on magnification icon a second
time to turn off zoom mode. Then click on a point for each of the 20 peaks in
the pattern. You should have a plot that looks like this:

Step
3.3: Fit Peaks
As the peaks are initially
added to the table, the refine flag is set for the peak intensity. Fit the
individual peak intensities by using Peak Fitting/Peakfit
menu command. Provide a file name and the Rwp drops
to ~40% with a reasonable background level, but not good peak shapes.
Select the Instrument
Parameter tree item, select the refinement flag for U, V, W, X, Y and SH/L,
then select the Peak List tree entry again and use the Peak Fitting/Peakfit menu command. The fit improves a bit, but since the
peak positions have not been refined, a good fit is not to be expected. Click
on the refine column heading to the immediate right of the peak positions, then
select "Y" and "vary all" and again use the Peak Fitting/Peakfit
menu command. The fit improves significantly with an Rwp
value of ~8%. The fit shows very small difference plot:
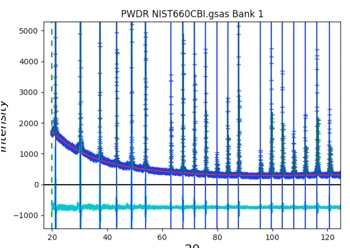
However, pressing the w key
in the plot window changes the plot appearance and it can be seen that the fit
at low angle is significantly worse than at high angle. This suggests that log
angle asymmetry may not be well fit.
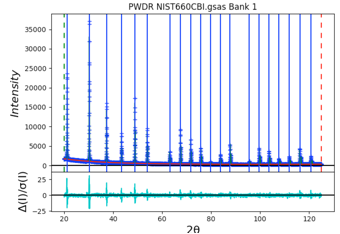
To improve this, we can force
the SH/L value to be larger. Instead of the local minimum that was found with
SH/L of ~0.003, we can select the Instrument Parameter tree item and set SH/L
to a larger value, say 0.03. Then select the Peak List tree entry again and use
the Peak Fitting/Peakfit menu command. The Rwp
improves somewhat, to circa 5%, but now the difference plot is greatly improved
at low angle with SH/L increasing to 0.063:
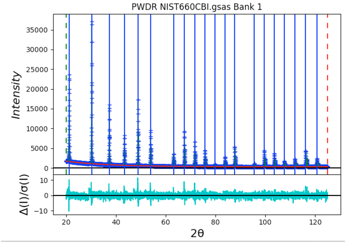
Step
3.4: Save Instrument Parameters
Select the Instrument
Parameter tree entry and then use the Operations/Save Profile... menu command to
write a file. This can be used as the starting point for future refinements.
The plot shown at this point compares the mostly meaningless default starting
profile terms (as solid lines) to the fit here (as dashed lines). Using Operations/Load
Profile... resets the default values to the current refinement parameters, which
makes for a simpler plot.
Step
3.5: Compare individual peaks widths to fit profile
While the Instrument
Parameter tree entry is selected, turn off refinement of the U, V, W X, and Y refinement
flags (SH/L can be left to continue to refine) and then select the Peak List
tree entry. Double-click on the
refine headings for the sigma and gamma columns to refine the individual peak widths
and again and use the Peak Fitting/Peakfit menu
command. The fit quality does not change very significantly, and selecting the Instrument
Parameter tree entry generates a plot that shows that the individual peak fits
are quite close to the fitted curves.